TEMA 4: ELECTRICITAT
TEMA 4: ELECTRICITAT
1) ¿Qué cantidad de electrones habrán atravesado un cable si la intensidad ha sido de 5 A
durante 30 minutos?
durante 30 minutos?
Q = I . t = 5 ·30 · 60 segundos = 9000 C
9000 · 6,24 ·10^18 = 5,62 . 10^22 electrones
2) Calcula la intensidad de corriente en microamperios, que circula por un cable si lo
atraviesan 2 . 1015 electrones en 6 segundos.
[(2·10^15) / (6,24·10^28)] / 6 = 5,34·10^ -5 A = 53,41 μA
3) Calcula la resistencia que tiene un cable de cobre de 200 m y diámetro de 4 mm..
El coeficiente de resistividad del cobre es 1,68 . 10-8 Ωm
El coeficiente de resistividad del cobre es 1,68 . 10-8 Ωm
(1,68·10^ -8 · 200) / (π·0,0022) = 0,267 Ω
4) Una chapa de plata de sección rectangular, ancho 2,5 cm. y alto 1 cm., tiene una longitud
de 25 cm., ¿Cuál es la resistencia que tiene si la resistividad de la plata es de 1,59 . 10-8
Ωm?.
de 25 cm., ¿Cuál es la resistencia que tiene si la resistividad de la plata es de 1,59 . 10-8
Ωm?.
(1,59·10^ -8 · 0,25) / 0,00025 = 1,59 .10-5 Ω
5) ¿Qué longitud deberá tener un hilo de cobre si su diámetro es de 0,4 mm y queremos que
ofrezca una resistencia de 10 Ω?
El coeficiente de resistividad del cobre es 1,68 . 10-8 Ωm
ofrezca una resistencia de 10 Ω?
El coeficiente de resistividad del cobre es 1,68 . 10-8 Ωm
La sección se calcula con la siguiente fórmula
S= π · 0,0002^2 puesto que está en milímetros y tienes que pasarlo a metros.
La S= 1,256^ -7
10Ω = p· (L/s)
S= π · 0,0002^2 puesto que está en milímetros y tienes que pasarlo a metros.
La S= 1,256^ -7
10Ω = p· (L/s)
10/p = L/ s
(10/ 1,68. 10^ -8) = L/ 1,256^ -7
L= (10·1,256^ -7)/ 1,68·10^-8) = 74,76 metros
L= (10·1,256^ -7)/ 1,68·10^-8) = 74,76 metros
6) Calcula la resistencia de una lámpara por la que circula una corriente de 0,7 A si se halla
sometida a un voltaje de 18 V.
sometida a un voltaje de 18 V.
18 = R·0,7
R = 18/0,7
R = 25,7 Ω
7) Calcula la intensidad de corriente que atraviesa la bombilla en el siguiente circuito
9 = 100·I
I = 9/100
I = 0,09 A = 90 mA
8) Si un equipo de música es de 60 W y estás escuchando música 5 h, ¿Cuántos kWh ha
consumido?. Sabiendo que 1 kWh cuesta actualmente 0,12 €, ¿en cuánto has incrementado
la factura de la electricidad?
consumido?. Sabiendo que 1 kWh cuesta actualmente 0,12 €, ¿en cuánto has incrementado
la factura de la electricidad?
0,3 kWh·0,12 €/ kWh = 0,036 €
9) En una bombilla leemos en el casquillo los siguientes datos: 220 V; 60 W
a) ¿Qué intensidad circulará al conectarla a 220 V?
b) Si la tenemos encendida durante 10 h ¿Cuántos kWh consume?
a) ¿Qué intensidad circulará al conectarla a 220 V?
b) Si la tenemos encendida durante 10 h ¿Cuántos kWh consume?
a)
60 = 220·I
I = 60/220 = 0,27 A
b)
E = 60·10 = 600 Wh = 0,6 kWh
10) Calcula la carga almacenada en un condensador de capacidad 10 μF que está conectado a
una batería de 24 V
una batería de 24 V
10 μF = 10·10^-6 F
Q = C·V = 10·10^-6 ·24 = 0,00024 C = 2,4·10^-4 C
11) a) Calcula la carga que adquiere un condensador de 20 μF
conectado a una batería de 12 V.
b) Si se conecta a una resistencia de 100 K,
calcula la constante de tiempo y el tiempo total de carga.
c) Dibuja la gráfica de carga
d) Indica el código de colores de la resistencia
SOLUCIÓN
a) C = Q / U Q = C·U = 20·10^-6 · 12 = 2, 4·10^-4 C
b) t = R·C = 100 · 1000 · 20·10^-6 = 2 s (tiempo en alcanzar el 63.2 % del voltaje de la fuente
12·0,632 = 7,58 V)
c)
d) 100 K = 100.000Ω Marrón - Negro - Amarillo
12) Calcular en el siguiente circuito:
a) Constante de carga del condensador.
b) Constante de descarga del condensador.
c) Tiempo de carga del condensador.
d) Tiempo de descargar del condensador.
e) Gráfica de la carga y descarga del condensador.
f) Indica el código de colores de las resistencias
a) Constante de carga del condensador.
b) Constante de descarga del condensador.
c) Tiempo de carga del condensador.
d) Tiempo de descargar del condensador.
e) Gráfica de la carga y descarga del condensador.
f) Indica el código de colores de las resistencias
SOLUCIÓN
a) t = R·C = 10 · 1000 · 2·10^-6 = 0,02 s (tiempo en alcanzar el 63.2 % del voltaje de la
fuente 9. 0,632 = 5,7 V)
fuente 9. 0,632 = 5,7 V)
b) t = R·C = 20 · 1000 · 2·10^-6 = 0,04 s (tiempo en descargarse llegando al 36.8 %
de su capacidad)
c) T = 5 R·C = 5·0,02 = 0,1 s (tiempo total de carga del condensador)
d) T = 5 R·C = 5·0,04 = 0,2 s (tiempo total de descarga del condensador)
e)
f) 10 K = 10.000Ω Marrón - Negro - Naranja
20 K = 10.000Ω Rojo - Negro - Naranja
13) Dos condensadores de 60 μF se conectan en paralelo y se alimentan con una batería de 12
V. La carga de los mismos se realiza a través de una resistencia de 70 K.
V. La carga de los mismos se realiza a través de una resistencia de 70 K.
a) Calcula la capacidad del condensador equivalente
C = C1 + C2 = 60 + 60 = 120 μF
b) Calcula la carga total que adquiere
Q = C.U = 120·10^-6 ·12 = 0,00144 C
c) Calcula el tiempo que tardan en cargarse
T = 5 R·C = 5· 70· 1000· 120.10-6 = 42 s
d) Dibuja el circuito
e) Dibuja la gráfica de carga
f) Indica el código de colores de la resistencia
70 K = 70.000Ω Violeta - Negro - Naranja
14) Explica el funcionamiento del circuito según las posiciones del conmutador
Cuando el conmutador está en la posición superior el condensador se carga y se enciende el LED
verde. Cuando el condensador se carga totalmente deja de pasar corriente eléctrica y el LED verde
se apaga.
Cuando el conmutador está en la posición inferior el condensador se descarga y se enciende el LED
rojo, hasta que se descarga totalmente y el LED rojo se apaga.
15) En el circuito de la figura se pide:
a) Pon el nombre de cada elemento
b) ¿Qué ocurre cuando activamos "I1"
c) ¿Qué ocurre cuando activamos "I1" e "I2"
d) ¿Qué ocurre cuando activamos "I1" e "I3"
e) ¿Para qué se utilizan las resistencias de 50 y 300 Ω
f) ¿Qué tensión pasa por la bombilla y por el zumbador?
a)
I1- Interruptor
I2- Conmutador
I3- Pulsador NC
a- Bombilla
b- Resistencia de 50 Ω
c- Motor
d- Zumbador
e- Relé de 1 conmutador
f- Resistencia de 300 Ω
g- Diodo LED
b) Cuando cerramos I1 se enciende la bombilla, giran los dos motores y se activa la bobina del relé y su conmutador cambia de posición, apagándose el diodo led
c) Cuando cerramos I1 y cambiamos la posición de I2 se enciende la bombilla, giran los dos motores y suena el zumbador
d) Cuando cerramos I1 y abrimos el pulsador I3 (el conmutador I2 permanece en la
posición superior), se enciende la bombilla, giran los dos motores y no pasa corriente por la bobina del relé y su conmutador permanece en la posición inicial, y se enciende el diodo led
e) Por los dos pasan 9 V, igual que por cada una de las ramas de paralelo
f) Son resistencias y se utilizan como divisores de tensión, es decir su función es
proteger a los elementos con los que se conectan en serie para que por ellos pase
menos voltaje del que manda.
EJERCICIOS DE ELECTRICIDAD
1.- CONCEPTOS BÁSICOS
1) Calcula la intensidad que circula por una resistencia de 30 Ω conectada a un generador de 15 V.
I = 30/15
I = 0,5 A
2) Calcula el voltaje al que hay que conectar una resistencia de 27 Ω para que pase por ella una intensidad de 3 A.
3 = V/27
V = 3·27
V = 81 V
3 = 15/R
3·R = 15
R = 15/3
R = 5 Ω
P = 15·3
P = 45 W consumidos
P Generada por la pila = 45 W
4) ¿Qué resistencia tiene el filamento de una bombilla de 220 V y 60 W?
Con esta fórmula sacamos la intensidad
60 = 220·I
I = 60/220
I = 0,27 A
I = 0,27 A
Con esta fórmula sacamos la resistencia
0,27 = 220/ R
0,27·R = 220
R = 220/0,27
R = 806,6 Ω
5) Calcula la energía que consume la bombilla del ejercicio anterior si nos la dejamos conectada durante dos días. ¿Cuánto tendremos que pagar si la electricidad nos cuesta 0,11 €/KWh?
E = 60·48h
E = 2880 Wh = 2,88 KWh
Tendremos que pagar 2,88 KWh·0,11€ = 0,32€
6) La placa de características de un televisor indica 220 V, 4 A. Calcula cuánto cuesta tenerla encendida durante una hora si la electricidad cuesta 0,11 €/KWh.
Con esta fórmula sacamos la potencia
P = 220·4
P = 880 W
Con esta fórmula calculamos la energía
E = 880·1
E = 880 Wh = 0,88 KWh
Tendremos que pagar 0,88 KWh·0,11 € = 0,097 €
2.- CIRCUITOS EN SERIE
1) Calcula la intensidad que circula por el siguiente circuito:
La suma de las dos resistencias es la resistencia total
R = R1 + R2 = 3Ω + 5Ω = 8 Ω
I = 32/8 = 4 A
2) Calcula el voltaje al que está conectada una resistencia de 3 Ω si circula por ella una intensidad de 4 A. Repite el cálculo con una resistencia de 5 Ω por la que pasa 4 A.
I = V/R
V1 = I·R = 4·3 = 12 V
I = V/R
V2 = I·R = 4·5 = 20 V
3) Calcula la intensidad que circula por un circuito formado por una resistencia
de 15 Ω en serie con otra de 20 Ω. El generador tiene un voltaje de 100 V. ¿Qué
caída de tensión se produce en cada resistencia?
La suma de las resistencias es la resistencia total
R = R1 + R2 = 15Ω +20Ω = 35Ω
I = V/R
I = 100/35 = 2,86 A
E(15Ω) = I·R =2,86·15 = 42,75 V
E(20Ω) = I·R =2,86·20 = 57,2 V
4) ¿Qué potencia eléctrica produce el generador del ejercicio anterior? ¿Qué
potencia consume cada una de las resistencias?
P = 100·2,86 = 286 WP(15Ω) = 42,75·2,86 = 122,69 W
P(20Ω) = 57,2·2,86 = 163,59 W
5) Calcula la intensidad, la caída de tensión y la potencia que
consume cada una de las resistencias del siguiente circuito. ¿Qué
potencia eléctrica produce el generador?
La suma de las resistencias es la resistencia total
R = R1 + R2 + R3 = 10 + 20 +30 = 60 Ω
I = 240/60 = 4 A
E(10Ω) = I·R = 4·10 = 40 V
E(20Ω) = I·R = 4·20 = 80 V
E(30Ω) = I·R = 4·30 = 120 V
P(10Ω) = 40·4 = 160 W
P(20Ω) = 80·4 = 320 W
P(30Ω) = 120·4 = 480 W
6) Tenemos una lámpara de 30 Ω de resistencia situada a 290,7 m de distancia del enchufe más próximo, cuyo voltaje es de 220 V. Vamos a utilizar cables de cobre de resistividad ρ = 0,0172 ΩAmm2/m y sección de 1 mm2. Calcula:
a) La resistencia de los cables.
R= (0,0172·290,7) / 1 = 5Ω·2 = 10 Ω
b) La intensidad que circula.
La resistencia es la suma de la de la lámpara y la de los cables 30+10 = 40Ω
I = 220/40 = 5,5 A
c) La caída de tensión en los cables y el voltaje real al que funcionaría la lámpara.
E(cables) = I·R = 10·5,5 = 55 V
E(lámpara) = I·R = 30·5,5 = 165 V
7) Calcula la caída de tensión en cada una de las 50 bombillas idénticas de una guirnalda de Navidad,
sabiendo que se conecta a 220 V. ¿Qué intensidad circula por la ristra si cada bombillita consume 3 W? Es
correcto afirmar que cada lámpara de la ristra tiene una resistencia de 10 Ω.
La potencia total es 50 bombillas·3W = 150 W
150 = 220·I
I = 150/220
I = 0,68 A
E = 220/50 = 4,4 V (caída de tensión)
No es correcto afirmar esto porque:
R = 4,4/0,68
R = 6,47 Ω
3.- CIRCUITOS EN PARALELO
1) Calcula la intensidad que circula por una resistencia de 10 Ω conectada a un generador de 30 V. Repite los cálculos si la resistencia tuviera 15 Ω.
I(10Ω) = V/R = 30/10 = 3 A
I(15Ω) = V/R = 30/15 = 2 A
2) ¿Qué resistencia hay que conectar a una pila de 30 V para que circulara por ella una intensidad de 5 A?
5 = 30/ R
R = 30/5
R = 6 Ω
3) Comprueba que dos resistencias de 10 Ω y de 5 Ω en paralelo son equivalentes
a una única resistencia de 6 Ω, mediante la expresión:
Rt = R1·R2..../R1+R2...
Rt = (10·5) / (10+5)
Rt = 50/15 = 3,3 Ω
Podemos concluir que no son equivalentes a una sola resistencia de 6 Ω
4) ¿Cuál es la resistencia equivalente a dos resistencias de 3 Ω y de 4 Ω conectadas en paralelo?
Rt = (3·4) / (3+4)
Rt = 12/7 = 1,714 Ω
5) En el siguiente circuito, calcula la resistencia equivalente, y posteriormente la intensidad en cada resistencia.
Rt = R1·R2..../R1+R2...Rt = (6·4) / (6+4)
Rt = 24/10 = 2,4 Ω
I(6Ω) = V/R = 24/6 = 4 A
I(4Ω) = V/R = 24/4 = 6 A
6) En el siguiente circuito, calcula la resistencia equivalente, y posteriormente la
intensidad en cada resistencia.
I(3Ω) = 15/3 = 5 A
I(2Ω) = 15/2 = 7,5 A
I(5Ω) = 15/5 = 3 A
La suma de todas las intensidades es la intensidad total
It = 5+7,5+3 = 15,5 A
15,5 = 15/R
R = 15/15,5
R = 0,967 Ω
4.- CIRCUITOS MIXTOS
1) En el siguiente circuito, calcula la resistencia equivalente, y posteriormente la intensidad y la caída de tensión en cada resistencia.
RT = 1/6 + 1/4 = 5/12 = 2,4 ΩRT = 2,4 + 15 = 17,4 Ω
I = 35/17,4
I = 2,01 A
E(2-3) = I·R = 2,01·2,4 = 4,82 V
I(4Ω) = 4,82/4 = 1,204 A
I(6Ω) = 4,82/6 = 0,083 A
E(15Ω) = 15·2,01 = 30,15 V
RT = 1/15 + 1/30 = 1/10 = 10 Ω
RT = 30 + 10 = 40 Ω
I1 = 80/40 = 2 AI2 = I3 = 20/15 = 1,33 A
I4 = 20/30 = 0,66 A
E1 = I·R = 2·30 = 60 V
E2 = I·R = 1,33·10 = 13,3 V
E3 = I·R = 0,66·10 = 6,66 V
E4 = I·R = 2·10 = 20 A
3) En el siguiente circuito, calcula la resistencia equivalente, y posteriormente la intensidad y la caída de tensión en cada resistencia. Por último, calcula la potencia que genera la pila y la que consume cada resistencia.
RT = 1/4 + 1/6 = 5/12 = 2,4 Ω
RT = 3+5+2,4 = 10,4 Ω
I1 = 20/10,4 = 1,923 A
I1 = I4 = 1,923 A
I2 = 4,615/4 = 1,1538 A
I3 = 4,615/6 = 0,76 A
E1 = I·R = 1,923·3 = 5,769 V
E2-3 = I·R = 1,923·2,4 = 4,615 V
E4 = I·R = 1,923·5 = 9,615 V
P(PILA) = 20·1,923 = 38,46 W P4 = I^2·R = 1,923^2·5 = 18,43 W
P1 = I^2.R=1,923^2·3 = 11,0937 W
P2 = 4,615·1,1538 = 5,32 W
P3 = 4,615·0,76 = 3,5 W
4) En el siguiente circuito, calcula la resistencia equivalente, y posteriormente la intensidad y la caída de tensión en cada resistencia. Por último, calcula la potencia que genera la dínamo y la consumida en cada resistencia.
5) En el siguiente circuito, calcula la resistencia equivalente, y
posteriormente la intensidad y la caída de tensión en cada
resistencia. Por último, calcula la potencia que genera la pila y la
consumida en cada resistencia.
posteriormente la intensidad y la caída de tensión en cada
resistencia. Por último, calcula la potencia que genera la pila y la
consumida en cada resistencia.
5.- CIRCUITOS DE KIRCHHOFF
1 y 2) Calcula las intensidades de cada rama en cada una de las siguientes redes de Kirchhoff:
CIRCUITO 1
I1 = 1,42 A
I2 = 2,4 A
I3 = 3,82 A
CIRCUITO 2
I1 = -1,72 A
I2 = -1,63 A
I3 = 0,09 A
3) Calcula las intensidades en el siguiente circuito:a) Con el interruptor abierto.
b) Con el interruptor cerrado.
A)
Es un circuito en serie y la Intensidad es:
I1 = (12-9)/15 = 0,2 A
I2 = 0 A
I3 = (9-12)/15 = -0,2 A
B)
I1 = 0,93 A
I2 = 1,37 A
I3 = 0,439 A
4) Calcula las intensidades que circulan por cada una de las resistencias de la siguiente red de Kirchhoff. ¿Qué potencia genera cada pila? ¿Qué potencia consume cada resistencia? Comprueba que toda la potencia generada es igual a toda la potencia consumida.
I1 = 0,727 A
I2 = 0,909 A
I3 = 0,181 A
P(8V) = 8·0,727 = 5,816 WP(4V) = 4·0,181 = 0,724 W
P(GENERADA) = 6,54 W
V(6Ω) = 0,727·6 = 4,362 V ---------> P(6Ω) = 0,727·4,362 = 3,171 W
V(4Ω) = 0,909·4 = 3,636 V----------> P(4Ω) = 0.909·3,636 = 3,305 W
V(2Ω) = 0,181·2 = 0,362 V----------> P(2Ω) = 0,181·0,362 = 0,066 W
P(CONSUMIDA) = 6,54 W
5) Calcula las intensidades que circulan por cada una de las resistencias de la siguiente red de Kirchhoff. ¿Qué potencia genera cada pila? ¿Qué potencia consume cada resistencia?
I1 = 1,489 A
P(12V) = 1,489·12 = 17,868 W
P(6V) = -0,383·6 = -2,298 W
P(2V) = 1,106·2 = -2,212 W
P(3Ω) = 1,489^2 · 3 = 6,652 W
P(4Ω) = (-0,383)^2 · 4 = 0,586 W
P(5Ω) = 1,106^2 · 5 = 6,611 W
P(8V) = 8·0,727 = 5,816 WP(4V) = 4·0,181 = 0,724 W
P(GENERADA) = 6,54 W
V(6Ω) = 0,727·6 = 4,362 V ---------> P(6Ω) = 0,727·4,362 = 3,171 W
V(4Ω) = 0,909·4 = 3,636 V----------> P(4Ω) = 0.909·3,636 = 3,305 W
V(2Ω) = 0,181·2 = 0,362 V----------> P(2Ω) = 0,181·0,362 = 0,066 W
P(CONSUMIDA) = 6,54 W
5) Calcula las intensidades que circulan por cada una de las resistencias de la siguiente red de Kirchhoff. ¿Qué potencia genera cada pila? ¿Qué potencia consume cada resistencia?
I1 = 1,489 A
I2 = 1,106 A
I3 = -0,383 A
P(6V) = -0,383·6 = -2,298 W
P(2V) = 1,106·2 = -2,212 W
P(3Ω) = 1,489^2 · 3 = 6,652 W
P(4Ω) = (-0,383)^2 · 4 = 0,586 W
P(5Ω) = 1,106^2 · 5 = 6,611 W
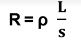
Comentarios
Publicar un comentario